Tag der Mathematik 2012

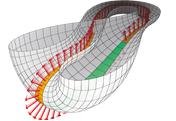
Die Kleinsche Flasche

Als Erkennungszeichen für den „Tag der Mathematik“ haben wir in diesem Jahr ein Bild einer halben Kleinschen Flasche gewählt (siehe oben rechts). Im Folgenden erläutert Ihnen Elmar Vogt, Professor für Mathematik an der Freien Universität Berlin, was es mit der Kleinschen Flasche auf sich hat.

„Bereits vor fast hundert Jahren ist von A. L. F. Meister ... eine Abhandlung erschienen, deren Gegenstand die Bestimmung des Inhaltes eines ebenen Vielecks in größtmöglicher Allgemeinheit ist, indem hier auch solche Vielecke in Betracht gezogen werden, deren Perimeter sich selbst ein oder mehrere Male schneiden. [Anmerkung: Hierbei werden einige umschlossene Bereiche mehrfach oder auch negativ gezählt, je nachdem wie oft sie im positiven oder negativen Sinn umlaufen werden.]
Nicht mit gleicher Allgemeinheit ist man bis jetzt bei Polyëdern zu Werke gegangen, sondern hat nur in einigen speciellen Fällen den Inhalt auch solcher Polyëder ermittelt, deren Oberflächen sich selbst schneiden. Denn hätte man die Eigenthümlichkeiten von Polyëdern dieser Art in ihrem ganzen Umfang durchforscht, so würde man auf den bis jetzt wohl noch nicht ausgesprochenen Satz gekommen sein, dass sich Polyëder konstruieren lassen, deren Inhalt gar nicht angebbar ist.“

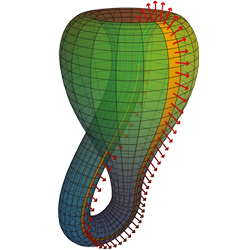
So die Einleitung eines Aufsatzes von August Ferdinand Möbius aus dem Jahr 1865, in dem, wahrscheinlich zum ersten Mal, nicht orientierbare Flächen ohne Rand beschrieben und behandelt wurden. Flächen ohne Selbstdurchdringung im dreidimensionalen Raum haben stets ein Äußeres und Inneres, so dass man das Volumen des Inneren bestimmen kann. Lässt man Selbstdurchdringungen zu, so stellte Möbius mit Überraschung fest, dass es Flächen ohne Rand gibt, von deren einer Seite man auf die andere gelangt, ohne die Fläche durchstoßen zu müssen. Sie haben also überhaupt kein Inneres.

In Möbius' Aufsatz finden wir auch eine Beschreibung des sogenannten Möbiusbandes, das man erhält, wenn man einen länglichen rechteckigen Papierstreifen an seinen gegenüberliegenden kurzen Streifen nach einer Drehung um 180 Grad verklebt. Dies war aber schon deutlich früher z. B. von Listing beschrieben worden, und es würde mich nicht überraschen, wenn es nicht, ohne ihm größere Bedeutung zuzumessen, Jahrhunderte zuvor schon betrachtet wurde.

Möbius gibt aber Flächen ohne Rand, allerdings mit Selbstdurchdringung, an. Ein explizites Beispiel war eine Fläche, die aus dem Möbiusband durch Anheften einer Kreisscheibe an dessen Rand ensteht. Er vermerkt, dass dies wohl die einfachste „einseitige“ Fläche sei. Diese Fläche ist die projektive Ebene. Allerdings hat das Möbius nicht vermerkt. Sie ist etwas schwieriger zu veranschaulichen als das Logo des diesjährigen Tages der Mathematik. Unsere Fläche ist die nach Felix Klein benannte Kleinsche Flasche, eine einseitige Fläche, die durch Aneinanderkleben zweier Möbiusbänder entlang ihrer Ränder entsteht.

Die halbe Kleinsche Flasche sehen wir rechts oben, das heißt, wir sehen das eine Möbiusband, aber mit Selbstdurchringung. Das zweite wird einfach spiegelbildlich oben angeklebt. Am Bild sieht man deutlich, wie man entlang einer geschlossenen Kurve von der einen Seite auf die andere gelangt.

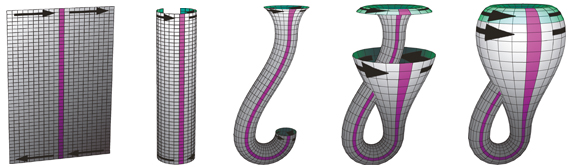
Ohne Selbstdurchdringung können wir uns die Kleinsche Flasche vorstellen, wenn wir uns vier Dimensionen gönnen. Das wusste übrigends auch Klein schon. Wie man Punkte des dreidimensionalen Raum durch drei reelle Zahlen, die x-, y- und z-Koordinaten, bescheibt, so kodiert man Punkte im vierdimensionalen Raum durch vier reelle Zahlen. Der dreidimensionale Raum wird dann durch die Punkte beschrieben, deren vierte Koordinate Null ist. Bei der Konstruktion der Kleinschen Flasche durch Verbiegung, Durchschieben und Verheften der Enden eines Schlauchs (siehe Bild oben) muss man nur während man im dreidimensionalen Raum den Schlauch sich selbst durchdringen lässt, das Ende, das wir bewegen, kurz in die vierte Dimension anheben, also die vierte Koordinate für alle Punkte des Schlauchendes gleichmäßig etwas anheben und nach Überschreitung der Durchdringung wieder auf Null absenken, um, jetzt wieder zurück im dreidimensionalen Raum, anschließend wie vorher die Enden zu verheften.

Mit ein bisschen Übung kann man sich das einigermaßen vorstellen. Wer es nicht glauben will, den können wir leicht mit präzisen Gleichungen im vierdimensionalen Raum überzeugen.

Verlosung

Unter allen Wettbewerbsteilnehmern, die an der Preisverleihung am 5. Mai 2012 teilnehmen, verlosen wir zusätzlich als Sonderpreise gläserne Kleinsche Flaschen.