IMAGINARY
Mathematisches Forschungsinstitut Oberwolfach
Bilder aus der berühmten IMAGINARY-Ausstellung zeigen Visualisierungen von algebraischen Flächen. Idee dabei ist, die visuelle und ästhetische Komponente der Mathematik als Blickfang zu verwenden, um den Betrachtern mathematische Hintergründe zu erklären. Zu jeder Fläche gibt es eine Erklärungstafel mit Einblicken in die mathematischen Eigenschaften und die Erstellung des Bildes. So werden die wichtigen Elemente der Bilder, wie z. B. die Singularitäten, beschrieben.
Die Idee von IMAGINARY ist – wie der Name schon vermuten lässt - die visuelle und ästhetische Komponente der Mathematik als Blickfang zu verwenden, um den BesucherInnen mathematische Hintergründe auf interaktive Weise zu erklären. Das Imaginäre, Unvorstellbare der Mathematik wird verbildlicht, es wird zu Bildern (images), die auch selbst erzeugt werden können.

Zitrus – das „Imaginary“-Logo
Design: Herwig Hauser, Sebastian Gann
Die Gleichung x^2 + z^2 = y^3(1−y)^3 von Zitrus erscheint ebenso einfach wie die Figur selbst. Zwei spiegelsymmetrisch angeordnete Spitzen rotieren um die durch sie gehende Achse. Die durch Weglassen von (1−y)^3 vereinfachte Gleichung x^2 + z^2 = y^3 sorgt für genau eine Spitze und x^2 + z^2 = (1−y)^3 liefert das Spiegelbild. Beide sind unendlich ausgedehnte Flächen. Das Produkt auf der rechten Seite der ursprünglichen Gleichung bewirkt, dass Zitrus beschränkt bleibt. Man überlegt sich: Wird y dem Betrag nach größer als 1 und damit die rechte Seite negativ, so erlaubt die Gleichung keine reellen Lösungen für x und z.

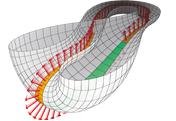
Miau
Design: Herwig Hauser, Sebastian Gann
Die Fläche Miau wurde durch Probieren auf einer eher eintönigen
Zugfahrt gefunden (Arbeiten mit algebraischer
Visualisierung lässt die Zeit sehr schnell vergehen). Die
Konstellation ist aber keineswegs zufällig – im Gegenteil,
wollte man für diese Fläche die algebraische Gleichung
systematisch herleiten, stieße man wohl auf unüberwindbare
Probleme.
Der Reiz von Miau ist natürlich die doppelte Öffnung mit
eingelagerter Singularität. Für den Mathematiker ist dies
eine Fundgrube, die geheimnisvolle Beziehung zwischen
Gleichung und Form zu erforschen.