Vorträge
Die Vorträge richten sich an ein breites Publikum. Sie zeigen insbesondere, wo und wie die Mathematik in unser Alltagsleben hineinreicht. Die Altersangaben in der folgenden (nach Klassenstufen und Alphabet sortierten) Liste sind nur als ungefähre Einordnung der wünschenswerten Vorkenntnisse zu verstehen.
Die Vorträge von Thomas Winter und Wolfgang König fallen wegen Erkrankung aus.
Parallel zum Wettbewerb gibt es am
Vormittag ein Programm
zur Lehrerfortbildung.
Hier geht es zum Zeit- und Raumplan.
Vorträge, empfohlen ab 7. Klasse (ab 13:00)
Was ist die Keplersche Fassregel und warum ist sie immer noch aktuell?
Prof. Dr. Diana Estévez Schwarz,
Berliner Hochschule für Technik
Zielgruppe: ab 7. Klasse Zeit: 15:00 Raum: L113
Wie man das Volumen einer Kugel oder
eines Zylinders ausrechnet, ist schon seit der Antike
bekannt. Das Volumen komplexerer Körper wird aber oftmals nur
geschätzt.
Im Jahr 1613 bemerkte Johannes Kepler bei den Vorbereitungen
seiner zweiten Hochzeit, dass die damals übliche Schätzung des
Fassvermögens von Weinfässern mit einer Messrute sehr ungenau
war. Daraufhin beschäftigte er sich mit der Volumenberechnung
von sogenannten Drehkörpern und veröffentlichte nur zwei Jahre
später eine deutlich bessere Vorgehensweise.
Im Vortrag wird seine Idee ausführlich erklärt und auch
verdeutlicht, warum sie noch heute bei vielen
computergestützten Berechnungen eine Rolle spielt. Die Ansätze
und Zusammenhänge werden vorwiegend bildlich dargestellt, so
dass Vorkenntnisse über den Flächeninhalt von Rechtecken und
Kreisen ausreichend sind.
Wen sollen wir impfen?
Prof. Dr. Marzena Fügenschuh,
Berliner Hochschule für Technik
Zielgruppe: ab 7. Klasse Zeit: 14:00 Raum: L113
Neue Technologien und
soziale Medien dringen schnell in jeden Aspekt unseres täglichen
Lebens ein und bieten uns großen Komfort für den Austausch von
Informationen und Meinungen. Wie sich neue Innovationen,
Verhaltensweisen und Krankheiten über soziale Netzwerke
verbreiten, ist eine der grundlegenden Fragestellungen der
Netzwerkwissenschaften. Darunter spielt das virale Marketing
eine bedeutende Rolle. Es ist eine Marketingtechnik, die die
Benutzer in einem sozialen Netzwerk dazu veranlasst, eine
Marketingbotschaft (viral ad) an andere weiterzuleiten, um den
größten Produktverkauf zu erzielen. Man möchte möglichst eine
kleine Gruppe von Erstanwendern finden, die durch Mundpropaganda
(WOM – word-of-mouth) die höchste Adoptionsrate im Netzwerk
erlangen. Insbesondere kann das virale Marketing benutzt werden,
um Gesundheitsprodukte gezielt zu verteilen und Wellen von
Ansteckungen vorzubeugen. Wen sollen wir denn impfen?

Hyperbolische Geometrie – Eine Welt mit nicht nur einer Parallelen
Carl O.R. Lutz,
AG Geometrie und mathematische Physik, Institut für Mathematik, Technische Universität Berlin
Zielgruppe: ab 7. Klasse Zeit: 13:00 Raum: L115
Das fünfte Postulat von
Euklid besagt, dass es in der Ebene zu einer Geraden und
einem Punkt stets genau eine zweite Gerade gibt, welche die
erste nicht schneidet und durch den gegebenen Punkt
verläuft. Bis weit in die Neuzeit hielten Mathematiker
dieses Postulat für eine natürliche Tatsache. Erst Arbeiten
von Nikolai I. Lobatschewski, Janos Bolyai und Carl F. Gauß
aus dem 19. Jahrhundert zeigten, dass eine Geometrie mit
unendlich vielen parallelen Geraden durch einen Punkt
ebenfalls sinnvoll ist. Aber wie sieht diese Geometrie aus?
Was sind ihre Eigenschaften? Und wie arbeiten Mathematiker
mit ihr? Dieser Vortrag lädt ein zu
einer Reise in eine parallele Welt.

Kann man neue Zahlen erfinden?
Dr. Marcus Weber,
Zuse-Institut Berlin
Zielgruppe: ab 7. Klasse Zeit: 13:00 Raum: HS2
Jeder Mensch lernt doch in
der Schule, was Zahlen sind. Na klar. Aber neben den Zahlen,
die wir zu kennen glauben, gibt es noch sehr viele andere
Zahlen, die im Laufe der letzten Jahrhunderte in der
Mathematik erfunden wurden. In dem Vortrag werden diese
Zahlen vorgestellt und auch, aus welcher Motivation heraus
sie erfunden wurden. Mal sehen, wie weit wir kommen werden:
Reelle Zahlen, imaginäre Zahlen, Quaternionen, hyperreelle
Zahlen, surreale Zahlen...

Kompression – die Mathematik hinter JPG und MP3
Dr. Martin Weiser,
Zuse-Institut Berlin
Zielgruppe: ab 7. Klasse Zeit: 14:00 Raum: HS2
Moderne Medien
überschütten uns mit einer Unmenge an Daten, die übertragen
und gespeichert werden müssen. Weil die Datenmenge fast noch
schneller wächst als Speicherkapazität und
Übertragungsbandbreite, werden die Daten komprimiert. Aber
wie funktioniert das eigentlich? Wie mißt man die
Informationsmenge in einem Musikstück? Und wieviel
Information steckt in einem Bild? Diesen Fragen gehen wir in
dem Vortrag nach.
Zaubern mit Mathematik
Erhard Zorn,
innoCampus, Institut für Mathematik, Technische Universität Berlin
Zielgruppe: ab 7. Klasse Zeit: 15:00 Raum: HS1b
Bei Zauberkunststücken denken die meisten an Tricks, die auf
Geschicklichkeit und Geschwindigkeit beruhen oder eine raffinierte Apparatur verwenden.
Wir schauen uns dagegen mathematische Zaubertricks an. Mit einfachen
Hilfsmitteln, wie einem Kartenspiel, lassen sich verblüffende Effekte
erzielen. Um die zugrunde liegende Mathematik zu verstehen, sind
Schulkenntnisse ausreichend.

Vorträge, empfohlen ab 9. Klasse (ab 13:00)
Die Suche nach einer Lösungsformel, die nie existierte
PD Dr. Dirk Kussin,
Fachgebiet Algorithmische Algebra, Institut für Mathematik, Technische Universität Berlin
Zielgruppe: ab 9. Klasse Zeit: 13:00 Raum: L116
Jeder kennt die pq-Formel
zum Lösen von quadratischen Gleichungen. Diese beschreibt,
wie sich die Lösung aus den Koeffizienten durch (Quadrat-)
Wurzelziehen ergibt. Das wussten schon die alten Babylonier
vor über 3500 Jahren. Ähnliche (kompliziertere)
Lösungsformeln für Gleichungen dritten und vierten Grades
wurden erst viel später in der Renaissance gefunden
(Fontana, Cardano bzw. Ferrari um 1535). Die Hoffnung danach
war groß, nun auch Formeln zu finden, die auf ähnliche
Weise (mit Hilfe von Wurzelziehen) die Lösungen von
Gleichungen vom Grad fünf oder höher beschreiben. Erst im
19. Jahrhundert gab es hierauf eine definitive Antwort, und
zwar eine negative! Es konnte bewiesen werden, dass eine
allgemeine solche Formel schon ab Grad fünf nicht mehr
existieren kann (Ruffini und Abel um 1824). Erst der junge
Évariste Galois (1811–1832) durchschaute dieses Problem um
1832 vollständig: er gab eine genaue Bedingung für eine
Gleichung an, wann eine derartige Lösung existiert und wann
nicht, bevor er mit nicht einmal 21 Jahren im Duell
starb. Mit seinen bahnbrechenden Ideen und Methoden war er
ein früher Wegbereiter der modernen Algebra.

„Verlust + Verlust = Gewinn“: Das Parrondo-Paradoxon
Dr. Stefanie Winkelmann,
Zuse-Institut Berlin
Zielgruppe: ab 9. Klasse Zeit: 14:00 Raum: L115
„Das ist nicht fair!“
Solch einen Satz hört man schon von kleinen Kindern, wenn
sie sich ungerecht behandelt fühlen. Die meisten Menschen
haben ein klares Gespür dafür, wann eine Situation oder ein
Spiel für sie fair oder unfair ist. Auf einen Münzwurf, bei
dem man entweder einen Euro gewinnt (bei „Kopf“) oder 100
Euro zahlen muss (bei „Zahl“) würde sich wohl kaum jemand
einlassen – schließlich ist der im Mittel zu erwartende
Verlust viel zu groß. Was aber, wenn man zwei solche
Verlustspiele zu einem Gewinnspiel kombinieren kann, indem
man sie abwechselnd spielt? Lassen sich dann quasi aus dem
Nichts Gewinne erzeugen und man kann beliebig reich
werden? In diesem Vortrag werden wir das sogenannte
Parrondo-Paradoxon untersuchen, bei dem der Wechsel zwischen
unvorteilhaften Situationen tatsächlich Vorteile bringt. Wir
definieren den Begriff der Fairness im mathematischen Sinne
und zeigen, wie man mithilfe der Mathematik ein wenig
Ordnung in die Welt des Zufalls bringen kann. Warum wir trotz
allem nicht ins Casino gehen und mit beliebigen Gewinnen
rechnen können, wird dabei ebenfalls geklärt.

Überbuchen: Balancieren von Nutzen und Risiken
Prof. Dr. Thomas Winter,
Berliner Hochschule für Technik
Zielgruppe: ab 9. Klasse Zeit: 15:00 Raum: L115
Oft hört man in den
Medien, dass Flugzeuge oder Hotels überbucht sind und dass
deswegen Passagiere aussteigen oder auf andere Hotels
ausweichen müssen. Teilweise sorgen die dazugehörigen
Kommentare für die Anbieter für einen Imageverlust. Warum also
sollten Fluggesellschaften oder andere Unternehmen das Risiko
in Kauf nehmen, Entschädigungszahlungen zu leisten und
ggf. einen Imageverlust zu erleiden? Wir betrachten das
Problem des Vorteils und Risikos von Überbuchungen aus
mathematischer Sicht mit Hilfe von Binomialverteilungen. Dabei
analysieren wir zunächst die Wahrscheinlichkeiten, dass es zu
einer Überbuchung und zu Entschädigungsleistungen kommt. Das
Risiko von Entschädigungen vergleichen wir dann mit dem
möglichen Gewinn der Vermeidung leerer Plätze im Falle von
Stornierungen. Am Ende erhalten wir eine Bewertung, wann sich
Überbuchungen in welchem Umfang lohnen könnten und welches
Risiko damit einhergeht.

Vorträge, empfohlen ab 11. Klasse (ab 13:00)
Von einsamen Läufern und verstellter Sicht
Ansgar Freyer,
AG Diskrete und Algorithmische Mathematik,
Institut für Mathematik,
Technische Universität Berlin
Zielgruppe: ab 11. Klasse Zeit: 14:00 Raum: L116
Die "Vermutung des
einsamen Läufers" lässt sich folgendermaßen formulieren:
Auf einer Rennstrecke mit Länge 1 laufen n Läufer. Alle Läufer
sind an der Start/Ziel-Linie gestartet und bewegen sich mit
verschiedenen konstanten Geschwindigkeiten. Wir sagen, dass
ein Läufer "einsam" ist, wenn er von jedem seiner Mitläufer
einen Abstand von mindestens 1/n hat. Ist jeder Läufer
irgendwann einsam?
Diese Vermutung geht zurück auf Jörg Wills, der sie im Jahr
1967 aufstellte, und ist bis heute ungelöst. Im Vortrag
überlegen wir uns, wie man so ein anschauliches Problem mit
mathematischen Mitteln angehen kann und stoßen dabei auf
schöne Ideen und interessante Umformulierungen der Vermutung.
Eine Einführung in die Spieltheorie
Prof. Dr. Max Klimm,
Diskrete Optimierung,
Institut für Mathematik,
Technische Universität Berlin
Zielgruppe: ab 11. Klasse Zeit: 15:00 Raum: KL29/111
Die Spieltheorie ist eine
mathematische Disziplin, die sich mit den Gesetzmäßigkeiten
strategischen Verhaltens beschäftigt. Dabei ist es nicht nur das
Ziel, optimale Strategien für echte Spiele wie Tic-Tac-Toe oder
Poker zu finden, sondern auch andere Situationen, in denen
Menschen strategisch handeln zu untersuchen. Beispielsweise
werden Autofahrer bei hohem Verkehrsaufkommen ihre Route so
auswählen, dass sie möglichst schnell ihr Ziel erreichen; bei
einer Online-Auktion wird versucht, andere Interessenten durch
die Abgabe eines möglichst guten Gebots zu überbieten. In diesem
Vortrag geben wir eine kurze Einführung in die Spieltheorie, in
der wir die wichtigsten Konzepte anhand von Beispielen
erläutern.
Bose-Einstein-Kondensation und ihre mathematischen Herausforderungen
Prof. Dr. Wolfgang König,
Weierstraß-Institut Berlin
Zielgruppe: ab 11. Klasse Zeit: 14:00 Raum: HS1b
Einer der spannendsten und
bisher am wenigsten verstandenen Phasenübergänge ist der
Kondensationseffekt, der 1924 von Albert Einstein und
Satyendranath Bose vorhergesagt und erst 1995 experimentell
realisiert wurde – bei Temperaturen sehr nahe am absoluten
Nullpunkt. Wir stellen den Effekt und seine Historie vor und
erläutern in einfachen Worten, warum die zugrundeliegende
Mathematik schwierig ist.
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben
Prof. Dr. Martin Oellrich,
Berliner Hochschule für Technik
Zielgruppe: ab 11. Klasse Zeit: 15:00 Raum: L116
Angewandte Mathematik durchdringt unsichtbar unseren technischen
Alltag. Ohne ihr reibungsloses Funktionieren hätten wir weder
Smartphones, Navis, Mobilfunk oder Internet, weder
Wahlhochrechnungen noch Wettervorhersage. Der weltweite Handel
wäre logistisch nicht zu bewältigen, es gäbe keine medizinischen
Diagnosen mit Computertomografie, keine faszinierenden Bilder
von anderen Planeten, keine Suchtreffer bei Google, keine
Kaufvorschläge bei Amazon.
Das sind nur die heutigen Erfolge. An allen Anwendungen wird
weiter geforscht und entwickelt. Anders gesagt: wem angewandte
Mathematik liegt und wer das Studium abschließt, hat praktisch
freie Jobwahl im oberen Einkommensbereich und abwechslungsreiche
Arbeitsinhalte.
In diesem Vortrag greife ich beispielhaft drei Bereiche der
angewandten Mathematik heraus:
- Statistik: Umgehen mit vielen Daten
- Numerik: Rechnen mit "echten" Zahlen
- Optimierung: alles rausholen mit System.
In drei überschaubaren Beispielen zeige ich, wie darin mathematische Ideen greifen. Und die sind –für hinreichend Interessierte– gar nicht schwierig zu verstehen. Ergänzend gebe ich Informationen, wo man in und um Berlin Mathematik in diverser Ausrichtung studieren kann. Dabei gehe ich auch auf die Unterschiede zwischen Universitäten und Fachhochschulen ein.

Funktionen von Funktionen
Dr. D.R.M. (Michiel) Renger,
Weierstraß-Institut Berlin
Zielgruppe: ab 11. Klasse Zeit: 13:00 Raum: KL29/111
Wir kennen die
mathematische Funktion als ein Objekt, das Zahlen auf Zahlen
abbildet. Aber wie wäre es, wenn wir eine Funktion haben, die
nicht Zahlen sondern Funktionen auf Zahlen abbildet? Diese
sogenannten "Funktionale" spielen eine wichtige Rolle in der
höheren Mathematik, und insbesonders die "stetigen linearen"
Funktionale. Das könnte natürlich sehr kompliziert werden,
aber zum Glück gibt es den Satz von Riesz ...
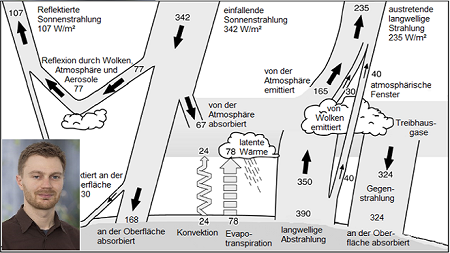
Klimawandel in einer Gleichung
Keno Riechers,
Potsdam Institut für Klimafolgenforschung
Zielgruppe: ab 11. Klasse Zeit: 15:00 Raum: HS2
Der von Menschen verursachte Klimawandel ist eines der
wichtigsten Themen der heutigen Zeit. Um ihn zu berechnen
nutzen Forscherinnen und Forscher Computermodelle, die so
kompliziert sind, dass sie nur auf Computern von der Größe
eines ganzen Hauses ausgeführt werden können. Doch selbst
diese Modelle lassen viele Details unbeantwortet. Der
Klimawandel ist also wahnsinnig kompliziert, einerseits!
Andererseits, sind die fundamentalen physikalischen
Prinzipien, die ihm zugrunde liegen, relativ simpel. In
meinem Vortrag möchte ich dieses ‘andererseits’ des
Klimawandels vorstellen. Denn bereits in einer einzigen
Gleichung lässt sich das Grundprinzip des Klimawandels
erkennen und verstehen. Diese Gleichung – ein sogenanntes
Energy Balance Model der Erde – wurde bereits 1969
hergeleitet und ist ein wichtiger Ausgangspunkt für die
moderne Klimaforschung. Sie basiert darauf, dass die Erde
pro Zeiteinheit die gleiche Menge an Energie an das
Universum abgeben muss, wie sie von der Sonne aufnimmt –
ansonsten verändert sich die Temperatur auf der Erde.
Die Energie der Sonne erreicht unsere Erde in Form von
Licht. Sie wird vielfach umgewandelt, lässt Pflanzen wachsen,
Wasser verdunsten, und Stürme entstehen. Am Ende muss diese
Energie das Erdsystem aber auch wieder verlassen – sonst würde
mit der Zeit die Gesamtmenge der Energie im Erdsystem immer
größer werden. Die Luft würde immer wärmer und Stürme immer
heftiger werden. Die Erde gibt Energie vor allem in Form von
Wärmestrahlung ab und wie viel Energie pro Zeiteinheit
abgegeben werden kann, hängt von der Temperatur der Erde
ab. Die Temperatur der Erde muss also so sein, dass die
abgegebene Wärmeenergie pro Zeiteinheit mit der aufgenommenen
Sonnenenergie pro Zeiteinheit übereinstimmt. Ausgehend von
diesen Überlegungen lässt sich das Energy Balance Model von
Budyko formulieren. Durch einen kleinen Trick lässt sich das
CO2, dass wir Menschen täglich ausstoßen, in die Gleichung
einbauen. Dann wird auf einen Blick klar, warum mehr CO2 in
der Atmosphäre eine höhere Temperatur auf der Erde bedeutet.
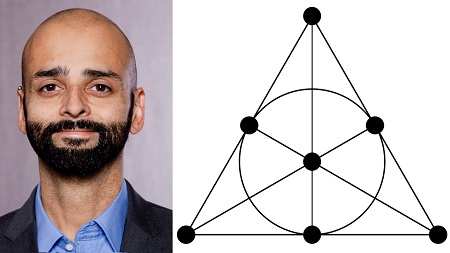
Punkt? Gerade? Dobble!
Prof. Dr. Raman Sanyal,
Institut für Mathematik,
Goethe-Universität Frankfurt am Main
Zielgruppe: ab 11. Klasse Zeit: 13:00 Raum: HS1b
Das Kartenspiel “Dobble”
besteht aus 55 Karten. Auf jeder Karte sind 8 Symbole und je
zwei Karten haben genau ein Symbol gemeinsam. Beim Spiel müssen
die Spieler zu zwei gegebenen Karten das gemeinsame Symbol
finden. Ein sehr spassiges aber hektisches Spiel. Die Frage die
mich mal über den Vater eines Klassenkameraden meines Sohnes
erreichte ist wie viele verschiedene Symbole es denn im Spiel
gibt. Mit ein bisschen Zeit und Geduld lässt sich das
beantworten aber die eigentliche Frage ist wie man so ein Spiel
wie Dobble konstruiert. Geht es auch mit 6 oder 9 Symbolen pro
Karte? Wenn ja, wie viele Symbole braucht man dann? Es stellt
sich heraus, dass wir solche Spiele mit etwas Geometrie
konstruieren können. Dazu müssen wir uns allerdings etwas locker
machen was unsere Anschauung von Punkten und Geraden betrifft.
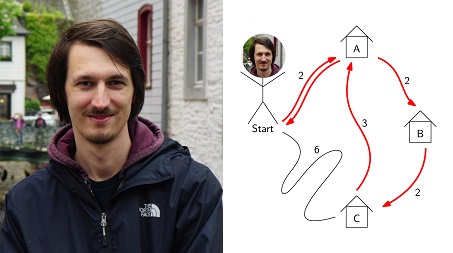
Ein Einblick in die Kombinatorische Optimierung und in die
Kombinatorische Geometrie
Dr. rer. nat. Dipl.-Ing. Manfred Scheucher,
AG Diskrete Mathematik,
Institut für Mathematik,
Technische Universität Berlin
Zielgruppe: ab 11. Klasse Zeit: 13:00 Raum: L113
Zwei klassische Beispiele
aus der kombinatorischen Optimierung sind die Bestimmung von
optimalen Reiserouten und die Minimierung von Kreuzungen in
Netzwerken. Während ersteres eine zentrale Rolle in der modernen
Logistik spielt und zweiteres in der Verkehrsplanung bzw.
Computerchipherstellung, gehören beide zu den großen ungelösten
Problemen der theoretischen Informatik.
Für viele solche Optimierungsprobleme ist nur dierelative Lage der
Objekte/Destinationen zueinander entscheidend, die expliziten
Koordinaten sind dabei jedoch irrelevant. Um die
dahinterliegenden kombinatorischen Strukturen besser zu
verstehen, beschäftigen wir uns in diesem Vortrag mit
sogenannten "Arrangements" von geometrischen Objekten (wie
Punkte, Linie und Kreise) und nehmen deren Kombinatorik etwas
genauer unter die Lupe.
Paradoxa mit reellen Zahlen
Dr. Holger Stephan,
Weierstraß-Institut für angewandte Analysis und Stochastik
Zielgruppe: ab 11. Klasse Zeit: 14:00 Raum: KL29/111
Bei der
Zahlenbereichserweiterung, wie wir sie in der Schule gelernt
haben, waren die Übergänge von einem Bereich zum anderen anfangs
einfach zu verstehen. So etwa der Übergang von den natürlichen
zu den ganzen oder gebrochenen Zahlen um alle Gleichungen der
Form a+x=b bzw. a x = b lösen zu können. Einfach zu verstehen
war auch, daß es auf der Zahlengeraden Punkte mit irrationalen
Koordinaten gibt, wie die Lösung der Gleichung x²=2.
Der Übergang zu reellen Zahlen mit Dedekindschen Schnitten, die
Einführung der Grenzwerte und ihre Untersuchung mit Epsilon und
Delta sind dagegen für einen normalen Schüler weitgehend
unmöglich zu verstehen. Daran schloß sich der Begriff der
Stetigkeit von Funktionen an. Der war eigentlich sehr
intuitiv. Eine Funktion ist stetig, wenn man zum Zeichnen den
Bleistift nicht absetzen muß. Die Definition über den Grenzwert
machte diese schöne Vorstellung wieder zunichte.
Versucht man die Zahlen zur Beschreibung eines realen Problems
zu nutzen, wird die Diskrepanz zwischen Theorie und Intuition
noch deutlicher. Man stößt bei jedem Schritt auf Paradoxa, die
die erfolgreiche Anwendung der Mathematik äußerst schwer
machen. So kann man im allgemeinen zwar beweisen, daß zwei
reelle Zahlen ungleich sind, sollten sie jedoch gleich sein,
läßt sich das im allgemeinen nicht beweisen.
Warum ist das so? Warum wird die Mathematik mit der Einführung
der Analysis und ihrer Grundlage, der reellen Zahlen so schwer
und unverständlich?
Im Vortrag wird versucht auf diese Fragen eine Antwort zu geben
und es werden alternative Ideen, die reellen Zahlen zu
verstehen, vorgeschlagen.
Referenzen: Vortrag