Lehrerfortbildung
Die Veranstaltung "25. Berliner Tag der Mathematik" wird von der Senatsverwaltung für Bildung, Jugend und Familie als Lehrkräftefortbildung im Umfang von 3 Stunden (9:00-12:00) anerkannt. Sie ist unter der Kursnummer 22.1-104287 im Internetangebot der regionalen Fortbildung veröffentlicht.
Eine Teilnahmebescheinigung erhalten Sie am Tag der Mathematik im Foyer der Mensa.
Übersicht (alphabetisch)
Beachten Sie auch den folgenden Vortrag mit besonderem Unterrichtsbezug im Nachmittagsprogramm:
|
Hier geht es zum Zeit- und Raumplan
Vorträge und Workshops (ab 09:00)
Echte Infinitesimalrechnung – Analysis mit hyperreellen Zahlen
StD Peter Baumann
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 09:00 Raum: L115
Abraham
Robinson hat in den 1960er Jahren gezeigt, dass die reellen
Zahlen zum geordneten Körper der hyperreellen Zahlen
erweitert werden können. Dazu gehören insbesondere infinite
und infinitesimale Zahlen, die schon die Begründer der
Analysis intuitiv richtig und gewinnbringend verwendet
haben. Sie stehen nun als logisch einwandfrei begründetes,
zeitgemäßes mathematisches Werkzeug zur Verfügung.
Mit diesen hyperreellen Zahlen kann man einfach rechnen,
viele Sachverhalte lassen sich intuitiv und anschaulich
darstellen, und der Grenzwertbegriff ist damit überflüssig
geworden. Darüber hinaus stellen die hyperreellen Zahlen ein
konstruktives Werkzeug dar, mit dem auch die Regeln der
Analysis einfach errechnet werden können.
Im Workshop wird der Umgang mit hyperreellen Zahlen
exemplarisch mit direktem Bezug zum Unterricht dargestellt,
und die didaktischen Vorteile dieses Werkzeugs werden
aufgezeigt. Hier ist ein Link zu
umfangreichem weiterführendem Material zu diesem Vortrag.
Referenzen: Vortrag, Webseite Nichtstandardanalysis mit umfangreichem Material
Wie man in der Lotterie gewinnt
Prof. Dr. Christian Haase, Institut für Mathematik,
Freie Universität Berlin
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 09:00 Raum: L116
Im Jahr 2005 bemerkte eine Gruppe von MIT Studenten, dass man
in der beliebten WinFall Massachusetts State Lottery
gewinnen kann – natürlich nur mit der richtigen Strategie. Das
funktionierte so gut, dass sogar eine Firma, Random
Strategies Investments, LLC, gegründet wurde, die fünf Jahre erfolgreich
operierte, bis im Jahr 2010 die Regeln geändert wurden. Wie die Massachusetts State Lottery
funktionierte, warum es Situationen mit positiver
Gewinnwahrscheinlichkeit gab, und was das alles mit projektiver
Geometrie zu tun hat, das erklärt Christian Haase in diesem Vortrag.
Natürlich wird dabei auch eine Lotterie veranstaltet!
Referenzen: Vortrag, YouTube-Video von Jordan Ellenberg

Das Casio Classpad II im Mathematikunterricht
Tom
Herwig, Casio Deutschland
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 11:00 Raum: L116
Tom Herwig gibt in seinem Workshop einen Einblick in die
grundlegende Bedienung des ClassPad II und präsentiert
Lösungsvorschläge zu CAS-Abituraufgaben aus unterschiedlichen
Bundesländern der vergangenen Jahren.
Referenzen: Casio YouTube-Kanal mit Tutorials, Materialdatenbank

Umsteigen ohne Warten: Fahrplanoptimierung für den Mathematikunterricht
Dr. Niels Lindner,
Zuse-Institut Berlin
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 10:00 Raum: L115
Niels Lindner erklärt den Einsatz mathematischer Methoden in der
Verkehrsplanung. Der Fokus liegt dabei auf dem Modellieren und
Optimieren von Taktfahrplänen, wie sie bei vielen
Verkehrsunternehmen eingesetzt werden. Dies führt zu einem
interessanten Optimierungsproblem, das zahlreiche Facetten der
Graphentheorie und der kombinatorischen Optimierung
beinhaltet. Auf der praktischen Seite ist das Paradebeispiel die
mathematische Optimierung des Berliner U-Bahn-Fahrplans, bei der
verglichen mit der manuellen Planung sogar ein Zug eingespart
werden konnte.
Was sind Zahlen? Intuition vs. Axiomatik in der Mathematik
Dr. Holger Stephan,
Weierstraß-Institut für angewandte Analysis und Stochastik
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 10:00 Raum: L113
Die Zahlen gehören zu den ältesten und geläufigsten mathematischen
Objekten. Heute kann kaum ein Schüler nicht wenigstens ein bisschen rechnen.
Umso erstaunlicher ist es, dass die Zahlen erst in der 2. Hälfte des
19. Jahrhunderts axiomatisch begründet wurden.
Das betrifft nicht nur die reellen Zahlen, sondern sogar die natürlichen Zahlen.
Zu jener Zeit konnte man bereits partielle Differentialgleichungen lösen und
fehlerfrei mit komplexen Zahlen rechnen. Die klassische analytische Mechanik
war voll entwickelt und konnte sehr erfolgreich angewendet werden.
Offenbar muss man nicht genau wissen, was Zahlen (und andere mathematische
Objekte) sind, um sie fehlerfrei benutzen zu können.
Die strenge Axiomatik läuft in der Mathematik meistens gegen die Intuition.
Das führt zu diversen Paradoxa etwa im Umgang mit reellen Zahlen. So ist es zum
Beispiel prinzipiell stets möglich zu beweisen, dass zwei reelle Zahlen
ungleich sind, dagegen lässt es sich im allgemeinen nicht beweisen, dass
zwei reelle Zahlen gleich sind.
Das hat Konsequenzen für den Mathematikunterricht.
Schüler nähern sich der Mathematik natürlich intuitiv. Da ist es nicht
verwunderlich, dass sie oft Probleme beim Verständnis der mathematischen
Objekte haben, wenn sie axiomatisch eingeführt werden. Das wird besonders
deutlich bei der Einführung der reellen Zahlen mit Hilfe der Dedekindschen
Schnitte oder bei der Epsilon-Delta-Definition der Stetigkeit.
Im Vortrag werden die Unterschiede zwischen
Intuition und Axiomatik in der Mathematik an markanten Beispielen besprochen
und Vorschläge für einen intuitiveren Mathematikunterricht gemacht.
Referenzen: Vortrag, Notizen
Das Lemma von Burnside
cand. math. Sebastian Szymanek, Institut für Mathematik,
Freie Universität Berlin
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 11:00 Raum: L115
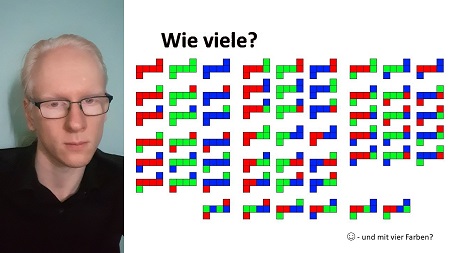
Manche Dinge lassen sich schwer zählen, weil sie mehr als eine Darstellungsform haben. Zum Beispiel
die Anzahl verschiedener Würfel, deren Seiten entweder rot, blau oder grün sind, oder die Anzahl
verschiedener Dreiklänge werden mit dem Lemma von Burnside berechnet werden. Dabei soll die Formel
nicht ohne Begründung vom Himmel fallen.
Referenzen: Vortrag, Ausarbeitung
Mein Hut, der hat vier Ecken… Mathematische Begriffsbildung entdeckend lernen
Dr. Benedikt Weygandt, Institut für Mathematik,
Freie Universität Berlin
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 09:00 Raum: L113
»Nenn es dann, wie du willst,/Nenn’s Glück! Herz! Liebe! Gott!/Ich habe keinen Namen/Dafür! Gefühl ist alles;/Name ist Schall und Rauch.«
In diesem Workshop widmen wir uns der Entstehung
mathematischer Begriffe und den Feinheiten der
Begriffsbildung. Faust mag so seine Schwierigkeiten mit dem
Definieren – oder der Beantwortung der Gretchenfrage? – gehabt
haben, und auch in der Mathematik ist Begriffsbildung
keineswegs trivial: Eine Definition ist schließlich mehr als
nur ein Name, aber zugleich auch keine vollkommen willkürliche
Verabredung. Und wenn ein Bild mehr als tausend Worte sagen
kann, dann erzeugt eine gute Definition auch mehr als tausend
Bilder in unseren Köpfen… Ziel des Workshops ist, Mathematik
nicht nur als ein fertiges Produkt mit kalkülhaften Rezepten
kennenzulernen, sondern den durch und durch kreativen Prozess
des Definierens einmal selbst zu erleben und dadurch auch für
den eigenen Unterricht nutzbar zu machen. Abschließend
reflektieren wir diesen Prozess und schauen, welche
Auswirkungen es haben kann, wenn man sich (bewusst oder
unbewusst) für die eine oder andere Definition eines
alltäglichen mathematischen Begriffs entscheidet – denn mit
großer Macht kommt schließlich große Verantwortung...

Maschinelles Lernen in Deinem Leben
Elias Wirth,
Technische Universität Berlin,
Zuse-Institut Berlin
Zielgruppe: für Lehrerinnen und Lehrer Zeit: 10:00 Raum: L116
Maschinelles Lernen verändert die Welt. Aber wie genau? Und
wie betrifft das Dich? In diesem Vortrag erkunden wir die
verschiedenen Bereiche des Alltags in denen maschinelles
Lernen bereits verankert ist: Von Krankheitsdiagnosen,
selbstfahrenden Autos, der Technologie hinter deinen
Spotifyvorschlägen, bis hin zu einem Gespräch mit einem echten
Transformer lernen wir dabei verschiedene Aspekte von
lernenden Algorithmen kennen.